最近在尝试将知识图谱融入NLP任务中,于是潜学了下GCN的算法以及各种变体,在这里做个总结,并附上pytorch版GCN代码。
什么是GCN
GCN论文中的公式多到吓人,但其实对于理解GCN原理来说,其中大多数都不必理会,本文也将抛开这些公式,从直观上讲述GCN的思想。
众所周知,GCN (图卷积神经网络) 就是将CV领域CNN的思想转移到图谱中。先回顾一下CNN的卷积结构:
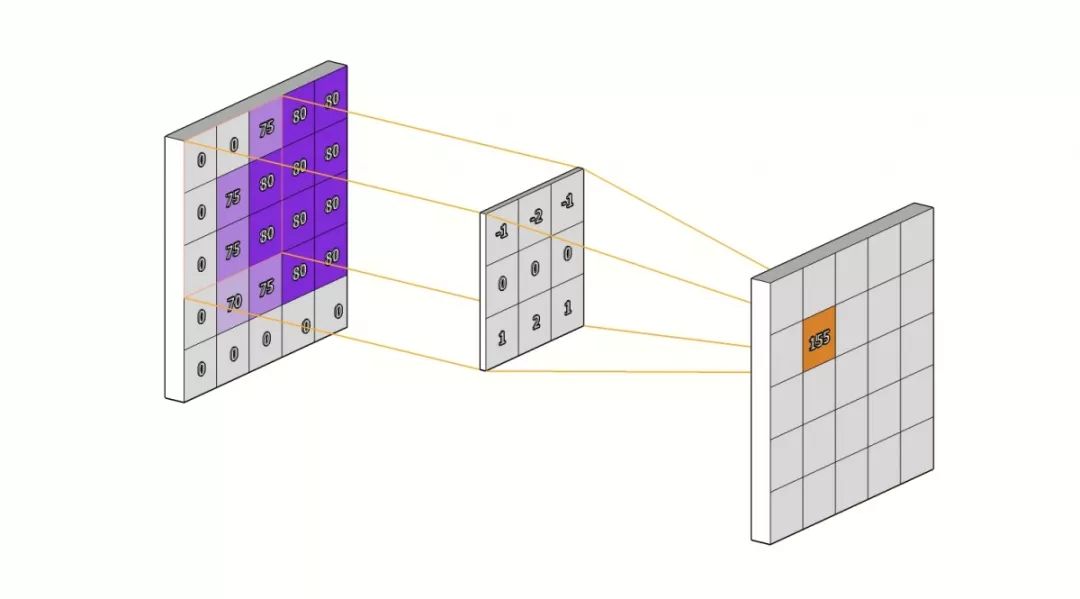
可以简单理解为对每个像素点利用卷积核汇聚其邻居像素点的特征生成新的像素点。
但对于图谱来说,图中每个节点都有不同的出度和入度,即每个节点的结构都是独一无二的,因此传统的CNN、RNN在图上根本起不了作用。GCN采取的解决办法其实很容易理解,既然CNN是聚合像素点邻居的特征,那对于图谱就可以聚合每个节点邻居节点的信息,CNN是利用卷积核卷积进行信息的聚合,而GCN也设计了一个公式用于聚合图节点的邻居特征,这一个公式就是整个GCN的核心。
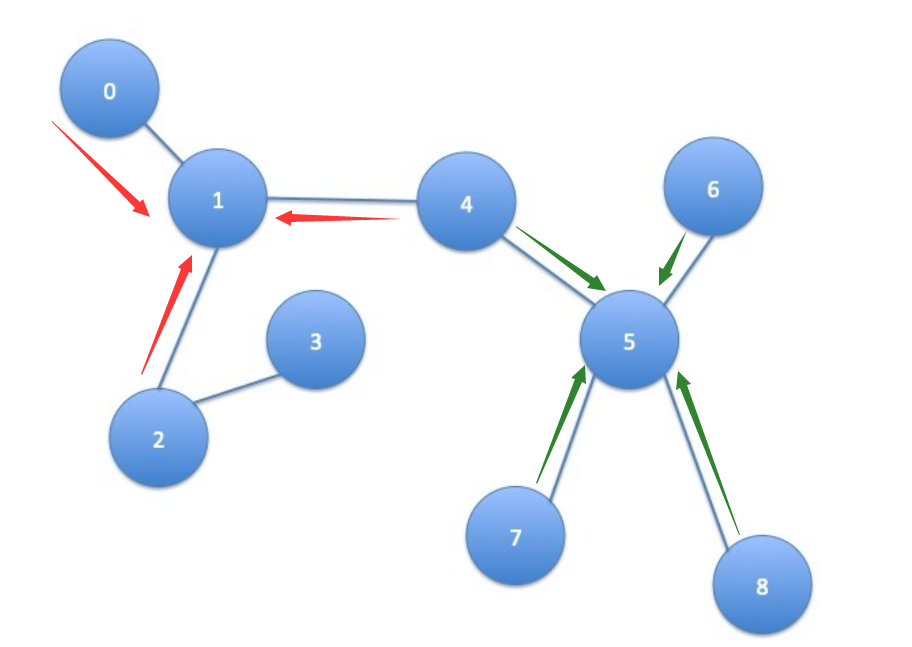
以上大概就是GCN的核心思想,至于为什么这样的图卷积方法可行,我认为是基于一个假设:图中节点的状态始终受其周围节点的影响,节点距离越近,影响越大。
GCN中的卷积
接下来看看GCN的核心公式,即聚合节点信息(卷积)的公式:
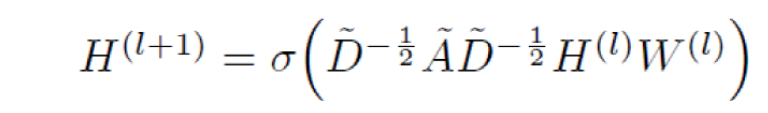
GCN也是一个和CNN相似的神经网络层,其中,
{
- 第一部分从作用上可以看作对图的结构特征的提取,即提取每个节点的邻居特征,再利用度矩阵求逆开方的方式对该特征进行归一化,该部分在图结构建好时即可直接求得。
- 第二部分即聚合图节点的邻居节点得到新的节点
- 第三部分即对新的节点进行线性变换,使该卷积变得可学习。
对于图卷积的分层可以这么理解,第一层的GCN只聚合了每个结点的邻居节点的特征,第二层GCN中目标节点的邻居节点以及聚合了其邻居的特征,此时对其特征进行聚合就相当于聚合了与目标节点距离为2的节点特征,所以k层的GCN网络相当于聚合了目标节点k跳的节点特征。
但由于并不是所有节点都会对目标节点产生影响,所以往往层数越高,GCN聚合到的噪音也越多,反而会影响最后的效率;同时,随着GCN网络的加深,节点的特征更容易趋向平滑,即每个节点的特征均十分类似,所以在实际使用中一般以2层GCN为最优。
更深的GCN
上文提到,GCN在层数增加时容易产生过平滑问题,但更深的网络往往能够学习到一些更底层的普适特征,为了让GCN能够进行更深的学习,不妨将CNN中网络加深的思想运用进来。本段就基于2019发表于ICCV的DeepGCNs介绍深层GCN的思想。
论文1:DeepGCNs
代码地址:github
DeepGCNs
DeepGCNs的思路很简单,就是将CNN中效果不错的skip-connection以及扩张聚合运用到GCN中。
- skip-connection(残差链接):就是RenNet中使用的残差链接,将该层的结果与上一层的输出(该层的输入)相加,能够很好的解决深层网络梯度消失/爆炸的问题,在这个基础上可以给链接加上可学习的权重(e.g.,ReZero)可以加速模型的收敛。在GCN中运用即将每层GCN的输出节点特征加上该层节点输入时的特征即可。
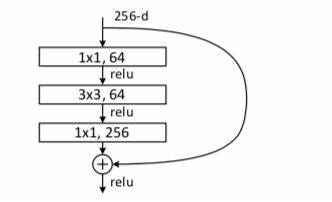
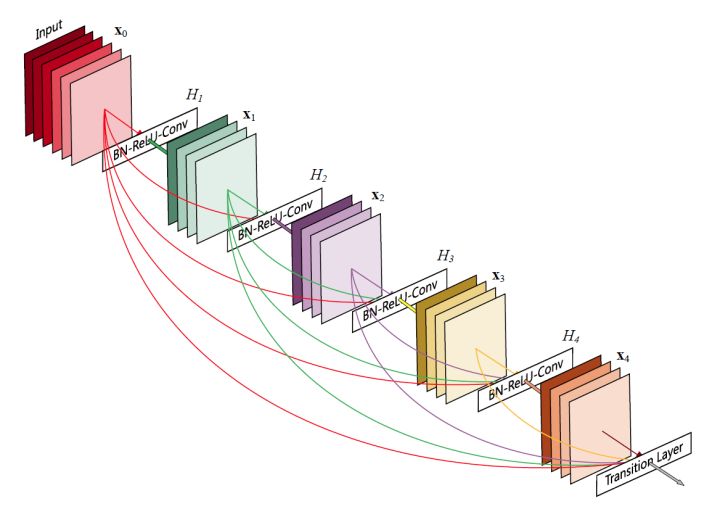
- skip-connection(密集连接):来源与DenseNet,每层的输入为之前所有层的输出的拼接,用公式表示就是
,为了防止网络变得过宽,一般DenseBlock的隐藏层输出维度会设的较小。
- 扩张聚合:将其他节点按距离进行排序编号,在聚合时按顺序每取一个节点就跳过d个节点,相当于扩大了节点的感知域。
论文在3D点积云数据集上进行实验,采用残差连接的深层GCN模型取得了较好的效果。